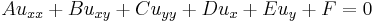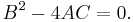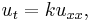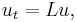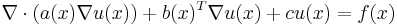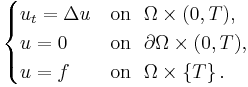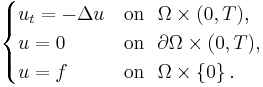Parabolic partial differential equation

A parabolic partial differential equation is a type of second-order partial differential equation (PDE), describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat diffusing through a solid.

A partial differential equation of the form

$Au_{xx} %2B Bu_{xy} %2B Cu_{yy} %2B Du_x %2B Eu_y %2B F = 0\,$

is parabolic if it satisfies the condition

$B^2 - 4AC = 0.\$

This definition is analogous to the definition of a planar parabola.

A simple example of a parabolic PDE is the one-dimensional heat equation,

$u_t = k u_{xx},\$

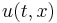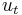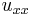where $u(t,x)$ is the temperature at time $t$ and at position $x$ , and $k$ is a constant. The symbol $u_t$ signifies the partial derivative with respect to the time variable $t$ , and similarly $u_{xx}$ is the second partial derivative with respect to $x$ .

This equation says roughly that the temperature at a given time and point will rise or fall at a rate proportional to the difference between the temperature at that point and the average temperature near that point. The quantity 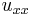$u_{xx}$ measures how far off the temperature is from satisfying the mean value property of harmonic functions.

A generalization of the heat equation is

$u_t = Lu,\$

where $L$ is a second order elliptic operator (implying $L$ must be positive also; a case where $L$ is non-positive is described below). Such a system can be hidden in an equation of the form

$\nabla \cdot (a(x) \nabla u(x)) %2B b(x)^T \nabla u(x) %2B cu(x) = f(x)$

if the matrix-valued function 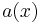$a(x)$ has a kernel of dimension 1.

1 Solution
2 Backward parabolic equation
3 Examples
4 See also
5 Notes
6 References

Solution

Under broad assumptions, parabolic PDEs as given above have solutions for all x,y and t>0. An equation of the form 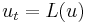$u_t = L(u)$ is considered to be parabolic if L is a (possibly nonlinear) function of u and its first and second derivatives, with some further conditions on L. With such a nonlinear parabolic differential equation, solutions exist for a short time but may explode in a singularity in a finite amount of time. Hence, the difficulty is in determining solutions for all time, or more generally studying the singularities that arise. This is in general quite difficult, as in the solution of the Poincaré conjecture via Ricci flow.

Backward parabolic equation

One may occasionally wish to consider PDEs of the form 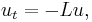$u_t = - Lu,\$ where $L$ is a positive elliptic operator. While these problems are no longer necessarily well-posed (solutions may grow unbounded in finite time, or not even exist), they occur when studying the reflection of singularities of solutions to various other PDEs^[1].

This class of equations is closely related to standard hyperbolic equations, which can be seen easily by considering the so-called 'backwards heat equation':

$\begin{cases} u_{t} = \Delta u & \textrm{on} \ \ \Omega \times (0,T), \\ u=0 & \textrm{on} \ \ \partial\Omega \times (0,T), \\ u = f & \textrm{on} \ \ \Omega \times \left \{ T \right \}. \end{cases}$

This is essentially the same as the backward hyperbolic equation:

$\begin{cases} u_{t} = -\Delta u & \textrm{on} \ \ \Omega \times (0,T), \\ u=0 & \textrm{on} \ \ \partial\Omega \times (0,T), \\ u = f & \textrm{on} \ \ \Omega \times \left \{ 0 \right \}. \end{cases}$

Examples

Notes

^ Taylor, M. E. (1975), "Reflection of singularities of solutions to systems of differential equations", Comm. Pure Appl. Math. 28 (4): 457–478, doi:10.1002/cpa.3160280403

References

Evans, Lawrence C. (2010) [1998], Partial differential equations, Graduate Studies in Mathematics, 19 (2nd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4974-3, MR 2597943, http://www.ams.org/bull/2000-37-03/.../S0273-0979-00-00868-5.pdf